数学家对期货的计算(数学家对期货的计算研究)

期货合约

期货合约是一种标准化的向前合约，规定了在未来特定日期购买或出售一定数量的标的资产的价格和数量。它是一种衍生品，其价值取决于标的资产的未来价格。

数学家对期货的计算

数学家通过构建数学模型来计算期货价格。这些模型考虑了各种因素，包括时间价值、无风险利率、市场波动率和标的资产未来价格的预期。

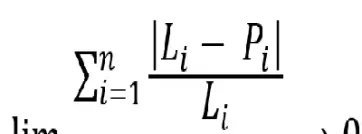
定价模型

1. Black-Scholes 定价模型

Black-Scholes 定价模型是计算欧式期权价格最常用的方法。它也被用于估算期货合约的价格，假设标的资产的未来价格服从对数正态分布。

2. Black 模型

Black 模型是 Black-Scholes 定价模型的一个简化版本，用于期货合约。它假设波动率是恒定的，并且不需要考虑期权的时间衰减。

3. Vasicek 模型

Vasicek 模型是一种随机利率模型，用来描述利率的未来变动。它可以用于计算利率期货合约的价格，假设利率服从反向 Ornstein-Uhlenbeck 过程。

风险评估

数学家使用风险度量来评估期货交易的风险。这些风险度量包括：

1. Delta

Delta 衡量期货价格对标的资产价格变化的敏感性。它表示当标的资产价格变化 1 个单位时，期货价格的变化数量。

2. Vega

Vega 衡量期货价格对市场波动率变化的敏感性。它表示当市场波动率变化 1 个百分点时，期货价格的变化数量。

交易策略

数学家还开发了基于数学模型的交易策略。这些策略旨在捕捉市场趋势或对沖風險。

1. 套利交易

套利交易涉及同时购买和出售同一标的资产的不同期货合约，以利用价格差异。

2. 统计套利

统计套利利用历史数据和回归分析来识别期货合约中具有统计优势的交易机会。

数学家对期货的计算涉及构建定价模型、评估风险和开发交易策略。这些计算为交易者和投资决策提供了有价值的依据。通过利用数学模型，数学家可以帮助投资者在期货市场中制定明智的决定。