期货套期保值线性规划实验报告(期货套期保值线性规划实验报告总结)

本实验报告了利用线性规划方法进行期货套期保值策略优化的实验过程及结果。实验旨在通过建立线性规划模型，模拟不同市场条件下，企业如何利用期货合约对现货价格风险进行有效管理。实验首先分析了企业面临的风险，包括现货价格波动风险、期货合约价格波动风险以及交易成本等。基于一定的假设条件，建立了线性规划模型，目标函数为最小化企业的总成本（包括现货采购成本、期货交易成本以及风险成本），约束条件则包括现货需求量、期货合约交易限额以及期货合约与现货合约的比例关系等。通过求解线性规划模型，得到了在不同情景下最优的套期保值策略，并对结果进行了分析和讨论，评估了不同策略在风险和成本方面的优劣，验证了线性规划方法在期货套期保值中的有效性。

模型构建与参数设定

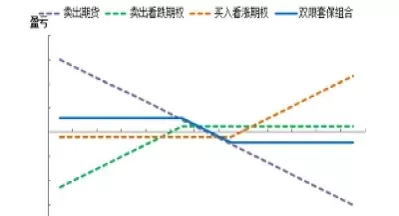
本实验的核心是构建一个精确的线性规划模型来模拟期货套期保值策略。模型的构建需要仔细考虑多个因素，包括：目标函数的设定，通常以最小化总成本为目标，总成本包含现货采购成本、期货交易成本（包括手续费、保证金利率等）、以及潜在的风险成本（可以用方差或标准差来衡量）。约束条件则需考虑企业的实际情况，例如：现货需求量、期货合约的交易限额（例如每日交易限额、持仓限额等）、期货合约与现货合约的比例关系（套期保值比例）、以及期货合约的交割日期等。参数设定方面，需要收集并整理历史价格数据，估计现货价格和期货价格的波动性、相关性等关键参数。这些参数的准确性直接影响模型结果的可靠性。参数的选取需要考虑历史数据代表性、市场环境变化等因素，并可能需要进行敏感性分析，以评估参数变化对模型结果的影响。

数据处理与模型求解

在模型构建完成后，需要对收集到的数据进行预处理。这包括数据的清洗、缺失值处理、异常值处理等。数据清洗是为了保证数据的准确性和完整性，去除错误或不合理的数据。缺失值处理则需要采用合适的插值方法或者剔除存在缺失值的数据。异常值处理则需要识别并处理数据中的异常点，避免这些异常点对模型结果产生不当影响。之后，利用线性规划求解器（例如，LINGO、MATLAB等）对建立的模型进行求解，得到最优的套期保值策略，即在给定约束条件下，达到目标函数最优值的期货合约买卖数量。求解结果通常包含最优的套期保值比例、期货合约的买入和卖出数量以及相应的总成本。

结果分析与策略评估

模型求解后，需要对结果进行详细分析和评估。分析最优套期保值策略下企业的总成本，并与不进行套期保值的情况进行比较，量化套期保值策略带来的成本节约或风险降低。分析不同参数变化对最优策略的影响，进行敏感性分析，评估模型的稳健性。例如，改变现货价格波动率、期货价格波动率、现货和期货价格的相关性等参数，观察最优策略和总成本的变化。需要结合实际市场情况，对实验结果进行讨论和解释，评估模型的适用性和局限性。如果模型结果与实际情况存在偏差，需要分析原因，并对模型进行改进。

模型改进与未来研究

实验结果可能并非完美地反映实际情况，因此需要对模型进行改进。例如，可以考虑加入更复杂的风险模型，例如考虑尾部风险（极端情况下的风险），并使用更鲁棒的风险度量指标，如条件风险价值（CVaR）。可以考虑将模型扩展到多商品、多品种的套期保值策略，以应对更复杂的市场环境。还可以考虑引入交易成本的动态变化，更加贴合实际交易情况。未来研究方向可以探索非线性规划模型在期货套期保值中的应用，以处理更复杂的市场关系和风险特征。还可以结合机器学习算法，例如神经网络或支持向量机，对未来价格进行预测，并将其融入到套期保值模型中，以提高预测精度和套期保值效果。更深入的研究可以探索如何将该模型应用于实际企业中，并结合企业具体的风险偏好和风险承受能力，制定更个性化的套期保值策略。

本实验报告详细阐述了利用线性规划方法进行期货套期保值策略优化的实验过程及结果。通过构建线性规划模型，模拟不同市场条件下企业的套期保值策略，并对结果进行了分析和评估。实验结果表明，线性规划方法可以有效地帮助企业制定最优的套期保值策略，降低风险并节约成本。模型的准确性和适用性依赖于参数的设定和模型的假设条件。未来研究需要进一步改进模型，以提高其准确性和适用性，并探索更复杂的套期保值策略。